Hyperbel
Keyword: Hyperbel
Links: Ellipse, Kreis, Parabel, Lemniskate, Polarität, Zwei
Definition: Eine Hyperbel ist eine zweigeteilte Kurve, deren beide Teile (Hyperbel-Äste) ins Unendliche geöffnet sind. Sie ist der geometrische Ort aller Punkte, für die gilt, dass die (positive) Differenz ihrer Abstände zu zwei verschiedenen Punkten F1 und F2 gleich groß ist. F1 und F2 werden Brennpunkte der Hyperbel genannt. AF1–AF2 = BF1–BF2 = CF2-CF1 = konst. (siehe Abb.1)
Information: Der Name Hyperbel stammt vom altgriechischen bállein „werfen“ und hyperballein „über das Ziel hinaus werfen“ und bezieht sich auf die sogenannte Exzentrizität ε, welche die Abweichung eines Kegelschnittes von der Kreisform beschreibt, und bei einer Hyperbel größer als 1 ist. (Der ε-Wert eines Kreises ist gleich 0, eine Ellipse hat einen ε-Wert zwischen 0 und 1 und der ε-Wert einer Parabel ist gleich 1.)
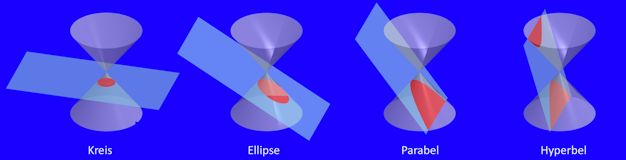
Die Hyperbel gehört wie der Kreis, die Ellipse und die Parabel zu den sogenannten Kegelschnittkurven. Das sind Kurven, die entstehen, wenn ein (Doppel-)kegel von einer Ebene geschnitten wird. Die vier Kurven gehen auseinander hervor: Wenn die Schnittebene sich dreht, werden aus dem Kreis Ellipsen, dann eine Parabel und dann Hyperbeln. Unter anderem entstehen Kegelschnittkurven bei der perspektivischen Abbildung eines Kreises. So wie auch die anderen Kegelschnittkurven Ellipse und Parabel findet man die Hyperbel in der Natur als „Spuren“ der vierten Dimension (Zeit oder Bewegung): Verfolgt man z.B. die Linie, die der Stab einer Sonnenuhr im Laufe eines Tages mit seinem Schatten „zeichnet“, dann bekommt man einen Hyperbel-Ast.
Das Prinzip der wechselseitigen Beziehung zwischen den beiden Brennpunkten, das bei der Ellipse anzutreffen ist, findet sich auch bei der Hyperbel, nur dass jeder Strahl einmal durch das Unendliche geht, bevor er auf den zweiten Brennpunkt trifft: Ein Strahl, der von einem Brennpunkt (z.B. F2) einer Hyperbel ausgeht, wird an der Hyperbelkurve reflektiert, um dann im Unendlichen zu verschwinden, auf der anderen Seite wieder aufzutauchen und den zweiten Brennpunkt (F1) zu treffen - und umgekehrt. (siehe Abb.2)
Bei der perspektivischen Abbildung eines Kreises erscheint als Abbild immer dann eine Hyperbel, wenn der Betrachtende sich in dem Kreis befindet: Je nach Blickwinkel erscheint der vor dem Betrachter liegende Teil des Kreises als nach unten gedrehter Hyperbel-Ast.
Im realen Leben können wir den hinter uns liegenden Teil des Kreises natürlich nicht sehen. Mathematisch konstruktiv betrachtet, lässt sich dieser Teil des Kreises aber durchaus abbilden: Er erscheint – sozusagen „von hinten durchs Auge aufs Bild projiziert“ - spiegelverkehrt über dem Horizont, als zweiter Hyperbel-Ast.Der Kreis „zerfällt“ also in der perspektivischen Abbildung in zwei Hyperbel-Äste – einen tatsächlich sichtbaren unten und einen seitenverkehrten, „irrealen“ oder „transzendenten“ oben. Dazwischen gibt es einen „Sprung“ durch das Unendliche von links unten nach rechts oben, von rechts unten nach links oben und umgekehrt.
In der Literatur spricht man von einer Hyperbel, wenn über das Glaubwürdige hinaus übertrieben wird.
Interpretation: Es ist immer wieder versucht worden, Gesetzmäßigkeiten der Mathematik, im übertragenen Sinne zu verstehen, besonders, wenn dabei der Aspekt der Unendlichkeit eine Rolle spielt. Nun basiert aber die Mathematik auf einer klaren Logik, die nur wahr oder falsch kennt und deshalb im Gegensatz zu symbolischen Betrachtungen steht, da diese eher ein Sowohl-als-auch–Denken benötigen. Insofern sind symbolische Betrachtungen von mathematischen Zeichen und Formeln mit besonderer Vorsicht zu sehen.
Die Form der Hyperbel - wie ein „nach außen gestülpter verzerrter Kreis“ – mit den zwei Brennpunkten, die durch die Hyperbeläste voneinander getrennt werden, zeigt auf den ersten Blick ein Bild der Zerrissenheit: zwei unvereinbare Gegensätze oder Polaritäten. Für jemanden, der in einer Situation so empfindet, könnte aber vielleicht das Wissen darum tröstlich sein, dass dieses Bild (die Hyperbel) ein Abbild einer Ganzheit (Kreis) in einer höheren Dimension ist: Ein Mensch, der mitten in etwas eigentlich Ganzem, Runden steht, kann davon nur einen Teil direkt wahrnehmen (das Sichtbare, das Bewusste, das Materielle, das Geschehene ...). Das „Ganze“ zerfällt in der Wahrnehmung in zwei Teile – einen realen und einen irrealen, einen materiellen und einem immateriellen, etc. -, die beide unendlich groß und durch das Unendliche miteinander verbunden sind.
Wenn der Mensch sich bewegt, also seinen Standpunkt verändert, oder die Blickrichtung wechselt, ändert sich das Bild der Hyperbel. Es kommt zu „Quantensprüngen“ in den Randbereichen: ein Punkt, der eben noch links unten war, erscheint plötzlich rechts oben und umgekehrt.
Jeder Punkt der Hyperbel ist bezogen auf zwei polare Brennpunkte. Das könnte veranschaulichen, dass es immer auch einen Bezug zum Gegenteil gibt, ob man es gerade wahrnimmt oder nicht. Je weiter wir in eine Richtung „über das Ziel hinaus werfen“, je extremer ist auch der Bezug zum Gegenpol.
Literatur: Standard; Wolfgang Haack, Darstellende Geometrie I-III, Sammlung Göschen de Gruyter; Rudolf Schmidt, Perspektive Schritt für Schritt, Bauverlag Wiesbaden und Berlin; Arnold Bernhard, Projektive Geometrie aus der Raumanschauung zeichnend entwickelt, Verlag Freies Geistesleben; www.kegelschnitte.de
Autor: Ernst, Christine